عدد حقيقي فائق

"*R" و "R*" يـُحوّلا إلى هنا. للاستخدامات الأخرى, انظر (توضيح).

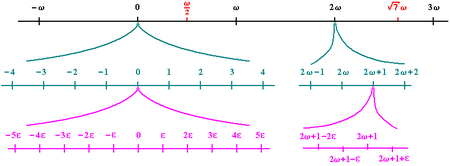
في الرياضيات ، سيما في التحليل غير القياسي، الأعداد الحقيقية الفائقة hyperreal numbers أو الحقيقيات غير القياسية nonstandard reals (تمثل عادة ب *R) هي حقل مرتب يعتبر امتدادا لحقل الأعداد الحقيقية المرتب R يحقق مبدأ النقل transfer principle . هذا المبدأ يتيح لنا اعادة تفسير مقولات الدرجة الأولى حول R على أنها صحيحة أيضا في *R .

Infinitesimals (ε) and infinities (ω) on the hyperreal number line (1/ε = ω/1)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

 الاستخدام في التحليل

 الحسبان مع دوال جبرية

Informal notations for non-real quantities have historically appeared in calculus in two contexts: as infinitesimals, like dx, and as the symbol ∞, used, for example, in limits of integration of improper integrals.

As an example of the transfer principle, the statement that for any nonzero number x, 2x ≠ x, is true for the real numbers, and it is in the form required by the transfer principle, so it is also true for the hyperreal numbers. This shows that it is not possible to use a generic symbol such as ∞ for all the infinite quantities in the hyperreal system; infinite quantities differ in magnitude from other infinite quantities, and infinitesimals from other infinitesimals.

Similarly, the casual use of 1/0 = ∞ is invalid, since the transfer principle applies to the statement that division by zero is undefined. The rigorous counterpart of such a calculation would be that if ε is a non-zero infinitesimal, then 1/ε is infinite.

For any finite hyperreal number x, its standard part, st(x), is defined as the unique real number that differs from it only infinitesimally. The derivative of a function y(x) is defined not as dy/dx but as the standard part of the corresponding difference quotient.

For example, to find the derivative f′(x) of the function f(x) = x², let dx be a non-zero infinitesimal. Then,

$f'(x)$	$=\operatorname {st} \left({\frac {f(x+dx)-f(x)}{dx}}\right)$
	$=\operatorname {st} \left({\frac {x^{2}+2x\cdot dx+(dx)^{2}-x^{2}}{dx}}\right)$
	$=\operatorname {st} \left({\frac {2x\cdot dx+(dx)^{2}}{dx}}\right)$
	$=\operatorname {st} \left({\frac {2x\cdot dx}{dx}}+{\frac {(dx)^{2}}{dx}}\right)$
	$=\operatorname {st} \left(2x+dx\right)$
	$=2x$

The use of the standard part in the definition of the derivative is a rigorous alternative to the traditional practice of neglecting the square of an infinitesimal quantity. Dual numbers are a number system based on this idea. After the third line of the differentiation above, the typical method from Newton through the 19th century would have been simply to discard the dx² term. In the hyperreal system, dx² ≠ 0, since dx is nonzero, and the transfer principle can be applied to the statement that the square of any nonzero number is nonzero. However, the quantity dx² is infinitesimally small compared to dx; that is, the hyperreal system contains a hierarchy of infinitesimal quantities.

 التكامل

One way of defining a definite integral in the hyperreal system is as the standard part of an infinite sum on a hyperfinite lattice defined as a, a + dx, a + 2dx, ..., a + ndx, where dx is infinitesimal, n is an infinite hypernatural, and the lower and upper bounds of integration are a and b = a + n dx.

 انظر أيضاً

• Constructive nonstandard analysis
• Hyperinteger
• Influence of nonstandard analysis
• Nonstandard calculus
• Real closed field
• Real line
• Surreal number - Surreal numbers are a much larger class of numbers, that contains the hyperreals as well as other classes of non-real numbers.

 للاستزادة

• Ball, W.W. Rouse (1960), A Short Account of the History of Mathematics (4th ed. [Reprint. Original publication: London: Macmillan & Co., 1908] ed.), New York: Dover Publications, pp. 50–62, ISBN 0-486-20630-0, https://archive.org/details/shortaccountofhi0000ball/page/50 
• Hatcher, William S. (1982) "Calculus is Algebra", American Mathematical Monthly 89: 362–370.
• Hewitt, Edwin (1948) Rings of real-valued continuous functions. I. Trans. Amer. Math. Soc. 64, 45—99.
• Jerison, Meyer; Gillman, Leonard (1976), Rings of continuous functions, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90198-5 
• Keisler, H. Jerome (1994) The hyperreal line. Real numbers, generalizations of the reals, and theories of continua, 207—237, Synthese Lib., 242, Kluwer Acad. Publ., Dordrecht.
• Kleinberg, Eugene M.; Henle, James M. (2003), Infinitesimal Calculus, New York: Dover Publications, ISBN 978-0-486-42886-4 

 وصلات خارجية

• Crowell, Calculus. A text using infinitesimals.
• Hermoso, Nonstandard Analysis and the Hyperreals. A gentle introduction.
• Keisler, Elementary Calculus: An Approach Using Infinitesimals. Includes an axiomatic treatment of the hyperreals, and is freely available under a Creative Commons license
• Stroyan, A Brief Introduction to Infinitesimal Calculus Lecture 1 Lecture 2 Lecture 3