سلسلة شتاينر

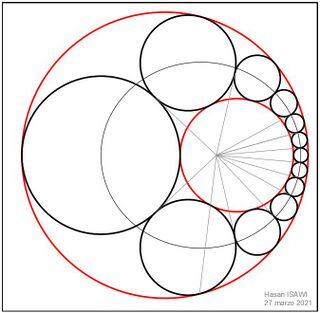
تشير سلسلة شتاينر(Steiner chain)، إلى سلسلة من الدوائر المتماسة لبعضها البعض. هذه الدوائر مرتبة بحيث يكون كل منها متماس لدائرتين متجاورتين. يمكن اعتبار سلسلة شتاينر امتدادًا لمشكلة القطوع المخروطية المماسية. ^[1]

تكون سلسلة شتاينر مغلقة عندما تكون الدائرتين الأولى والأخيرة متماسة لبعضهما البعض. يجب البدء بدائرتين غير متقاطعتين لبناء السلسلة. وهذا يعني ان الدائرة الأصغر يمكن ان تكون داخلية أو خارجية بالنسبة للدائرة الأكبر. في هذه الحالتين، تقع مراكز الدوائر المكونة للسلسلة على قطع ناقص أو قطع الزائد، على التوالي.

تمت تسمية سلسلة شتاينر نسبة للعالم السويسري ياكوب شتاينر، الذي عرفها في القرن التاسع عشر واكتشف العديد من خصائصها. كما يُنسب إليه الفضل في صياغة مسامية شتاينر.^[2] تنص على أنه إذا كانت هناك سلسلة مغلقة واحدة على الأقل من الدوائر المتماسة لدائرتين معلومتين، فإن هناك عدد لا حصر له من الدوائر الأخرى.^[3]

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

إجراء وصفي لتحديد سلسلة شتاينر باستخدام التعاكس

تم إعطاء دائرتين داخليتين ، Δ' و Δ" ، غير متحدة المركز. مطلوب تحديد سلسلة شتاينر. يتكون الإجراء مما يلي: - نستخدم طريقة التعاكس لتحويل Δ' و Δ" الى دائرتين Δ'* و Δ"* متحدتا المركز. - نقوم بإنشاء سلسلة من الدوائر المتماسة لبعضها البعض والمتماسة ايضا لـ Δ'* و Δ"*. هذه الدوائر تشكل سلسلة شتاينر. - نستخدم طريقة التعاكس مجددا لتحديد الدوائرة المتقابلة لـ Δ' و Δ".

من المهم معرفة ان التعاكس علاقة تقابلية، حيث تصطف النقاط المتقابلة مع مركز التعاكس؛ وتتلاقى الخطوط المتقابلة على محور التعاكس. في حالة الدوائر، يكون محور التعاكس غير نهائي لأن الاشكال المتقابلة مشابهة لبعضها البعض.^[4]

تعاكس دائرتين

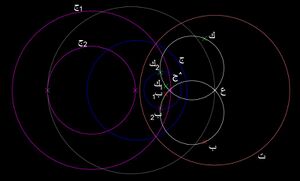
معلوم دائرتين (اللون الأحمر) متحدة المستوى، وبدون نقاط مشتركة بينهما، من الممكن دائما تحويلهما، عن طريق الانعكاس، إلى دائرتين متحدتي المركز.

الانشاءات الهندسية:

نأخذ في الاعتبار أي دائرتين ج وج^ (الشكل 3)؛ بلا نقاط مشتركة، والتي تحددان حزمة من الدوائر؛
نعين نقطة ب بحيث لا تنتمي إلى أي واحدة من الدائرتين
نفترض أن ب1 و ب2 هما انعكاس ب بالنسبة للدائرتين ج وج^
نرسم الدائرة س1 التي تمر بالنقاط ب، ب1 و ب2
وبطريقة مماثلة نرسم الدائرة س2 ، بحيث تمر بالنقاط ك، ك1 و ك2
نرسم دائرة ت بحيث يقع مركزها في نقطة التقاطع ع، بين الدائرتين س1 و س2
نحدد انعكاس الدائرتين ج، ج^ بالنسبة للدائرة ت وهكذا نحصل على دائرتين متحدتي المركز

الشكل 3

^[5]

معرض

انشاءات هندسية وصفية لرسم سلسلة شتاينر
اجراء هندسي وصفي لتحديد سلسلة شتاينر
سلسلة شتاينر ولكن بمخروطيات غير متشابهة
سلسلة شتاينر ولكن لأسطح إهليلجيه عامة (متقابلة اثنين اثنين لبعضها البعض)
إنشاءات هندسية وصفية لعملية تعاكس ( inversion) دائرة زرقاء بالنسبة لدائرة أخرى صفراء ، حيث الزرقاء لا تمر بمركز الصفراء
إجراء وصفي لتحديد سلسلة شتاينر باستخدام التعاكس

مراجع

^ The problem of tangency to three non-homothetic conics
^ تعريف البورمية في مفردات الموسوعة تريكاني (Treccani) Archived 2020-02-24 at the Wayback Machine
^ (EN) H.S.M. Coxeter, S.L. Greitzer, Geometry Revisited (PDF), in New Mathematical Library, vol. 19, The Mathematical Association of America, 1967, 124-125
^ مدونة الدكتور حسن العيسوي. سلسلة شتاينر (Steiner chain)
^ المرجع السابق

هذه بذرة مقالة عن الهندسة الرياضية تحتاج للنمو والتحسين، ساهم في إثرائها بالمشاركة في تحريرها.

[1] The problem of tangency to three non-homothetic conics

[2] تعريف البورمية في مفردات الموسوعة تريكاني (Treccani) Archived 2020-02-24 at the Wayback Machine

[3] (EN) H.S.M. Coxeter, S.L. Greitzer, Geometry Revisited (PDF), in New Mathematical Library, vol. 19, The Mathematical Association of America, 1967, 124-125

[4] مدونة الدكتور حسن العيسوي. سلسلة شتاينر (Steiner chain)

[5] المرجع السابق

[1]

[2]

[3]

[4]

[5]