دائرة التقبيل
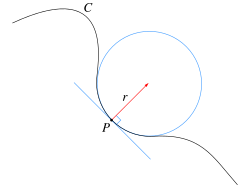
في الهندسة التفاضلية للمنحنيات، دائرة التقبيل إنگليزية: osculating circle لمنحني أملس عند نقطة من نقاطه هي دائرة مركزها يقع على الناظم الداخلي للمنحني وتكون درجة انحناء الدائرة مساوياً لدرجة انحناء المنحني عن نقطة التماس. هذه الدائرة من بين جميع الدوائر المماسة للمنحني عند نقطة معينة تكون أكثر الدوائر قرباً من المنحني فتبدو وكأنها تضم المنحني وتقبله لذلك أطلق عليها اسم دائرة التقبيل.
مركز هذه الدائرة ينطبق على مركز انحناء المنحني عند النقطة ذاتها، ونصف قطر الدائرة يكون مساوياً لنصف قطر انحناء المنحني عند ذات النقطة.
وصف رياضي
Let (s) be a regular parametric plane curve, where s is the arc length (the natural parameter). This determines the unit tangent vector T(s), the unit normal vector N(s), the signed curvature k(s) and the radius of curvature R(s) at each point for which s is composed:
Suppose that P is a point on γ where k ≠ 0. The corresponding center of curvature is the point Q at distance R along N, in the same direction if k is positive and in the opposite direction if k is negative. The circle with center at Q and with radius R is called the osculating circle to the curve γ at the point P.
If C is a regular space curve then the osculating circle is defined in a similar way, using the principal normal vector N. It lies in the osculating plane, the plane spanned by the tangent and principal normal vectors T and N at the point P.
The plane curve can also be given in a different regular parametrization
where regular means that for all . Then the formulas for the signed curvature k(t), the normal unit vector N(t), the radius of curvature R(t), and the center Q(t) of the osculating circle are
الإحداثيات الكارتيزية
We can obtain the center of the osculating circle in Cartesian coordinates if we substitute and for some f function. If we do the calculations the results for the X and Y coordinates of the center of the osculating circle are:
الخصائص
For a curve C given by a sufficiently smooth parametric equations (twice continuously differentiable), the osculating circle may be obtained by a limiting procedure: it is the limit of the circles passing through three distinct points on C as these points approach P.[2] This is entirely analogous to the construction of the tangent to a curve as a limit of the secant lines through pairs of distinct points on C approaching P.
The osculating circle S to a plane curve C at a regular point P can be characterized by the following properties:
- The circle S passes through P.
- The circle S and the curve C have the common tangent line at P, and therefore the common normal line.
- Close to P, the distance between the points of the curve C and the circle S in the normal direction decays as the cube or a higher power of the distance to P in the tangential direction.
This is usually expressed as "the curve and its osculating circle have the second or higher order contact" at P. Loosely speaking, the vector functions representing C and S agree together with their first and second derivatives at P.
If the derivative of the curvature with respect to s is nonzero at P then the osculating circle crosses the curve C at P. Points P at which the derivative of the curvature is zero are called vertices. If P is a vertex then C and its osculating circle have contact of order at least three. If, moreover, the curvature has a non-zero local maximum or minimum at P then the osculating circle touches the curve C at P but does not cross it.
The curve C may be obtained as the envelope of the one-parameter family of its osculating circles. Their centers, i.e. the centers of curvature, form another curve, called the evolute of C. Vertices of C correspond to singular points on its evolute.
أمثلة
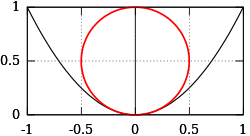
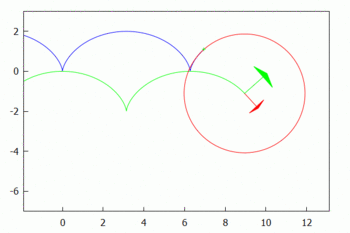
قطع مكافئ
لقطع مكافئ
the radius of curvature is
At the vertex the radius of curvature equals R(0)=0.5 (see figure). The parabola has fourth order contact with its osculating circle there. For large t the radius of curvature increases ~ t3, that is, the curve straightens more and more.
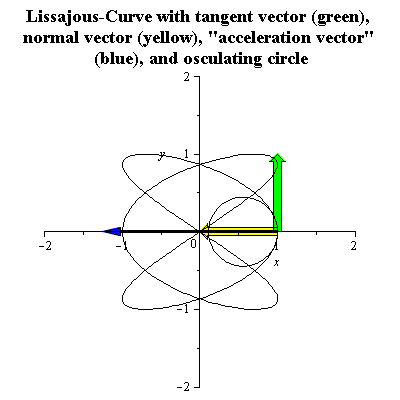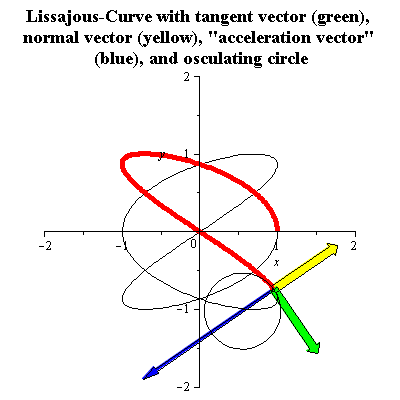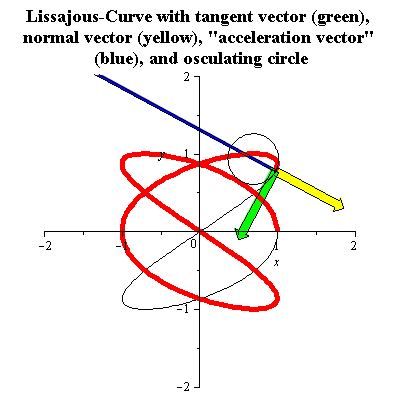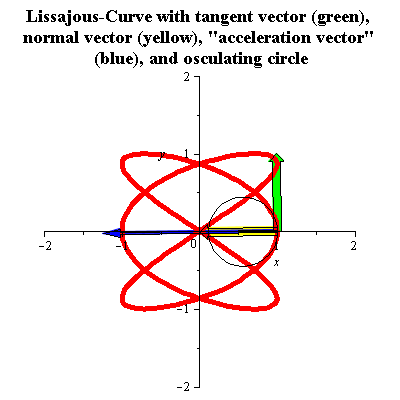
منحنى ليساجو
A Lissajous curve with ratio of frequencies (3:2) can be parametrized as follows
It has signed curvature k(t), normal unit vector N(t) and radius of curvature R(t) given by
و
See the figure for an animation. There the "acceleration vector" is the second derivative with respect to the arc length .
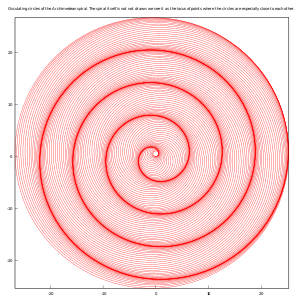
دويري
A cycloid with radius of r can be parametrized as follows:
Its curvature is given by the following formula:[3]
which gives:
انظر أيضاً
الهامش
- ^ Osculating curves: around the Tait-Kneser Theorem by E. Ghys, S. Tabachnikov, V. Timorin
- ^ Actually, point P plus two additional points, one on either side of P will do. See Lamb (on line): Horace Lamb (1897). An Elementary Course of Infinitesimal Calculus. University Press. p. 406.
- ^ Eric W. Weisstein, Cycloid at MathWorld.
للاستزادة
For some historical notes on the study of curvature, see
- Grattan-Guinness & H. J. M. Bos (2000). From the Calculus to Set Theory 1630-1910: An Introductory History. Princeton University Press. p. 72. ISBN 0-691-07082-2.
- Roy Porter, editor (2003). The Cambridge History of Science: v4 - Eighteenth Century Science. Cambridge University Press. p. 313. ISBN 0-521-57243-6.
{{cite book}}:|author=has generic name (help)
For application to maneuvering vehicles see
- JC Alexander and JH Maddocks (1988): On the maneuvering of vehicles doi:10.1137/0148002
- Murray S. Klamkin (1990). Problems in Applied Mathematics: selections from SIAM review. Society for Industrial and Applied Mathematics. p. 1. ISBN 0-89871-259-9.
وصلات خارجية